Parsing expressions

Expressions occur naturally in many languages, for instance in SQL. Usual ways of executing expressions are by interpretation or code generation. While I want to eventually talk about code generation, a sensible first step approaching expressions is parsing them from text which I will discuss in the blog post.

Looking at a SQL statement, we find multiple expression but will first focus on the one used to find qualifying tuples which comes after the WHERE keyword:

select * from lineitem
where l_orderkey < 200+50*7.5 and l_quantity > 9

While the expression given in this example might seem slightly manufactured, the takeaway is that such expressions can be

• nested,
• common operator precedence rules like addition binding less strongly then multiplication need to be observed, and
• types might need to be inferred.

Starting from the string representation of the expression, it must first be converted into a format which is suitable for further processing by a parser. While parsers can be hand-written, and some people argue that this is a good idea (e.g., here and here) it is definitely not a fast way to get started and hand-written parsers do not work well when the language definition is not quite clear in the beginning. This calls for a parser generator which takes a BNF-like description of the language to be read and converts it into a program which can then parse that language and trigger call backs or - ideally - generate an abstract syntax tree (AST) representing a input.

While tools exist which create a parser which has an AST as its output, I am not aware of any free, stable and up-to-date tool that generates a C++(11) AST. In java, I used ANTLR many years ago and it is capable of creating an AST and also specifying rewrite passes for that tree but unfortunately ANTLR is very heavyweight and does not sport a C++ (let alone C++11) generation target.

Wikipedia offers an extensive list of parser generators, however many are not maintained anymore. For my purposes, it seems like BISON would be a good contestant but I usually assume a smaller project size and language complexity so I frequently use less fancy parser generators based on parse expression grammer (PEG). For this blogpost, we will be using packcc (original version) because it is the only PEG based parser generator I am aware of which is capable of parsing left recursive grammars by implementing the approach mentioned in this paper from ACM SIGPLAN 2008.

Looking at the expression from the beginning of this post without the SQL boilerblate:

l_orderkey < 200+50*7.5 and l_quantity > 9

we will focus on simple arithmetics, comparisons and two types, int32_t and double. Writing a grammar acceptable by packcc starts out be defining helpful rules for skipping whitespace and detecting literal values:

literal_int        <- [0-9]+
literal_double     <- [0-9]+ '.' [0-9]+

_      <- [ \t\r\n]* ('--' [^\n]* '\n' [ \t\r\n]?)*
__     <- &[^a-zA-Z_] _

Since the parser generated by packcc is directly applied to the input string, there’s no tokenization step which takes care of converting all characters into neater tokens. Instead, we essentially define regular expressions for the building blocks of our language, in this case ints, doubles and whitespace. Naming the whitespace rule _ is convenient since it will be used around most rules in the program at each position where whitespace can be tolerated in the input. The additional whitespace rule named __ here is an extremely awkward detail of using a parse expression grammar parser generator. It means we will tolerate whitespace, however we do not tolerate 0 or more characters of white space but instead ask that there is at least one non character symbol. This is important to force parsing operators like or and and correctly without enforcing whitespace in many more places where it is not helpful.

Continuing with our grammar, let’s next express addition and multiplication:

op_cmp <- '<' / '>' / '='
op_add <- '+' / '-'
op_mul <- '*' / '/'
cmp    <- cmp _ op_cmp _ add
       /  add
add    <- add _ op_add _ mul
       /  mul
mul    <- mul _ op_mul _ prim
       /  prim
prim   <- literal_double / literal_int

These rules encapsulate both parsing of comparisons, additions and multiplcations as well as operator precedence. If possible, a comparison will be parsed first. If that does not work, we try to parse an addition which binds more strongly than a comparison. If that doesn’t work, we try to parse a multiplication, which binds even more strongly. If we can not parse a binary expression, then we will try parsing a prim which is currently either a literal integer or double. Note that the order in which prim is specified is important in PEG. Otherwise, we would parse the numbers before the decimal point as an integer and then fail to continue. The double has to be parsed first. In hindsight, not using PEGs and resorting to a GLR parser generator like BISON might help avoiding this kind of issue for more complex projects.

Bringing it all together, we add a top-level rule which parses an expression potentially surrounded by whitespace

expr <- _ add _

and some boilerplate and we have a first cut of our expression parser. Adding variables and more operations to this is straight-forward. Unfortunately though, the parser does not do anything intelligent with the input except determining whether it is in the language or not.

To convert the input string to something more usable, most yacc/bison style parser generators allow the grammar to be annotated with actions to be performed when parsing a particular rule succeeds. Many first expression examples use these annotations to implement a calculator. While this might look nice, it is not a scalable way of implementing anything on top of a parser. The way to go is to convert the input into a tree like representation, usually referred to as an abstract syntax tree. The idea is to convert each node into a tree node containing other tree nodes as its children, a representation closer to this:

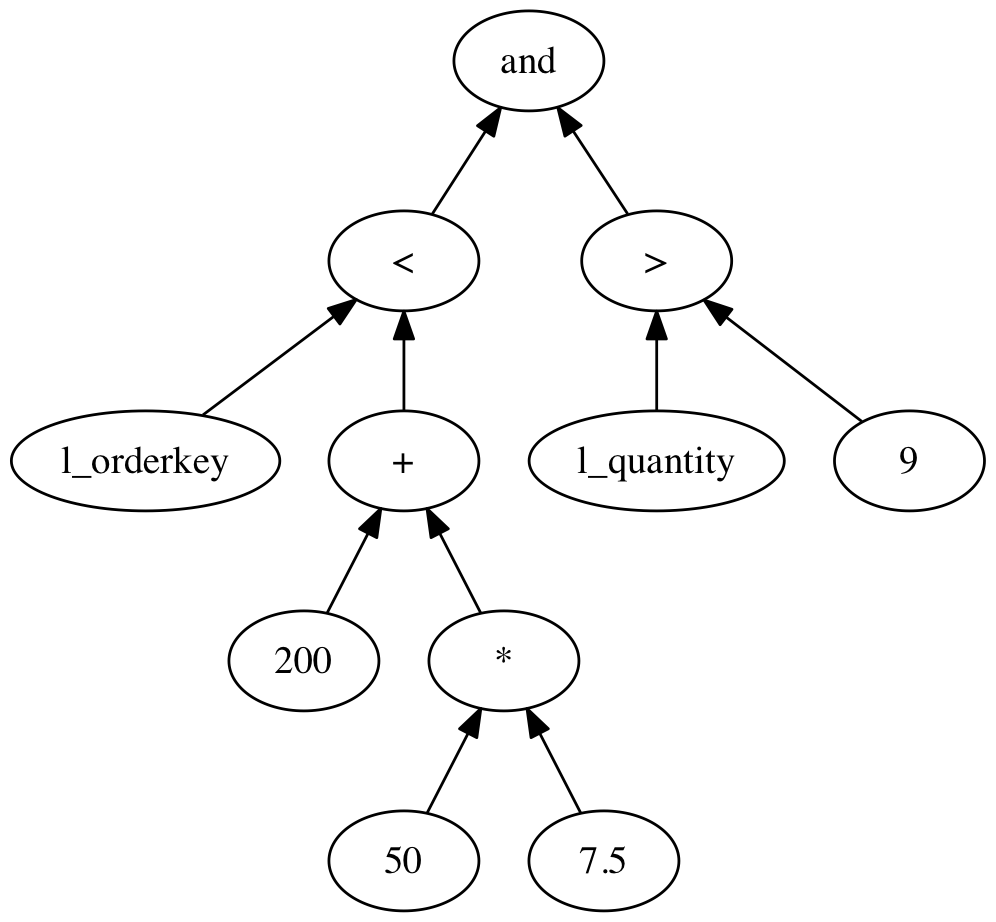
This tree structured representation of the parser expression can be implemented as a pointer structure between node classes, something similar to this:

struct Node {};
struct Binary : public Node { std::string op; Node* left; Node* right; };
struct LitInt : public Node { int value; }
struct LitDouble : public Node { double value; }

As a side-effect of parsing, using annotations to the grammer, this representation can be constructed and then much more easily handled in the remainder of the program. It usually pays of to write a generator for AST nodes since then infrastructure methods like dumping the tree to dot or adding the visitor pattern to the tree are less time consuming and new nodes can be added with ease. I hacked an AST node generator a couple of years ago but one can be easily hacked given a few hours of time.

Now that a simple expression is represented in a machine friendly format, we can focus on transforming, interpreting and code generating in upcoming posts. The dot example and the grammer with a tiny runner can be found here.